Criterios de aceptación de resistencias por debajo del f’c especificado en los planos estructurales
Artículo escrito por:
Ing. David Ricardo Chinchay Pujada (Especialista en Diseño Estructrural y miembro del equipo de FGE Consultores), CIP 106933.
Con frecuencia se recibe muchas consultas con respecto a la obtención de valores de resistencia del concreto, por debajo del especificado en los planos estructurales.
Es un lugar común que muchos supervisores soliciten y exijan que los contratistas hagan las demoliciones de aquellos elementos en los que se ha verificado que los ensayos de resistencia a la compresión dan valores por debajo del valor del f’c especificado.
Existen obviamente los ensayos de núcleos diamantinos para poder verificar si el concreto colocado es efectivamente menor.
Según la norma E-060 al sacar los núcleos diamantinos y poder aceptar el concreto se debe en simultáneo las siguientes condiciones según numeral 5.6.5.4 de la norma E-060:
1.-El promedio de los tres testigos extraídos deben ser igual o mayor que el 85% del f´c.
2.-Ningun testigo individual debe estar por debajo de 75% del f´c.
Si se cumplen las condiciones anteriores se aceptaría el concreto con las condiciones que se reformulen y/o corrijan el control de calidad del concreto.
Pero, ¿Qué hacemos cuando no se han cumplido las condiciones establecidas? ¿Es factible exigir la demolición de las estructuras?
En ninguna norma se establece la demolición de las estructuras.
En esto hace muy bien el reconocido Ing. Enrique Pasquel en sus ensayos “Entendiendo el concreto” en la que menciona que en estos caso solo el especialista estructural es el encargado de evaluar su diseño y establecer con las nuevas condiciones si esta aun apto la estructura para resistir las condiciones de carga a la que estará impuesta la estructura.
Para explicar la base del porqué aún podemos tener un margen de resistencia en una estructura en la que no se cumple el f´c, se basa en la filosofía de diseño en la cual diseñamos las estructuras de concreto.
Esta filosofía llamada LRFD (Load and Resistance Factor Design) se basa en procedimientos semiprobalisticos a través del estudio de muchas obras y ensayos de laboratorio.
En esta filosofía de diseño se tienen los siguientes principios:
- Reducción de la resistencia de los materiales teniendo en cuenta impresiones en las dimensiones de los elementos, errores constructivos, poco control de calidad en obra, etc.
- Amplificación de las cargas por imprecisiones en la estimación de las mismas, cambio de uso imprevisto, etc.
Con lo mencionado y de manera sencilla diseñamos para contemplar deficiencias constructivas y de diseño y sobre diseñamos pensando en que las cargas superarán las expectativas previstas.
Es decir; que aplicamos una incertidumbre basada en estudios estadísticos de muchas obras y ensayos de laboratorio a través de años.
Para darle un sustento matemático procederemos a calcular los factores de seguridad que nos da el método de rotura (como también se le llama al LRFD).
A continuación, presentamos la siguiente tabla de factores de reducción para distintas solicitaciones según nuestra norma E-060 -2009 vigente. (Nota en la próxima edición de esta norma se han modificado estos factores acorde a las ediciones más recientes de la norma ACI-318, pero para fines de este articulo usaremos nuestra norma vigente)

Los factores de seguridad que tiene el método LRFD se basan en poder determinar y correlacionar los factores de reducción y las cargas amplificadas.
Usaremos el ejemplo sencillo de una losa aligerada de 20 cm de espesor, con una sobrecarga de uso de 200 kg/m2.
Peso propio: 300 kg/m2
Piso terminado: 100 kg/m2
Sobrecarga: 200 kg/m2
Carga total en servicio: 300 + 100 + 200 = 600 kg/m2
Usando la primera combinación de carga y que implica las cargas gravedad:
Combinación 1: 1.4*CM + 1.7*CV
= 1.4*(400 kg/m2) + 1.7*(200 kg/m2) = 900 kg/m2
Dependiendo de la solicitación a evaluar se usa la siguiente expresión para el cálculo del factor de seguridad:
Coeficiente seguridad = (1/φ)*(carga amplificada/carga de servicio)
Coef. Seguridad a flexión = (1/0.9)*(900/600)= 1.67
Coef. Seguridad a corte = (1/0.85)*(900/600)= 1.76
En resumen, en un ejemplo sencillo como este; si se cumplen todas las condiciones de diseño y se procura un buen proceso constructivo nuestra estructura, en este caso una losa aligerada, tendrá 1.67 se seguridad a la flexión y 1.76 de seguridad al cortante.
Tambien pondremos a continuación un ejemplo de una edificación real en la que se ha diseñado todos sus elementos de acuerdo a la norma técnica de concreto armado.
Una vez entregado el proyecto, aprobado y en fase constructiva nos vienen con la consulta desesperada del contratista de obra en la que solicita la verificación con valores de concreto de 170 kg/cm2 el cual están por debajo incluso de los valores admisibles en la pruebas de diamantina.
Este concreto es el colocado en un eje de pórticos principales y exactamente corresponde al vaciado de viga y losa. El supervisor exige la demolición y no opta por otra solución. El ingeniero estructural toma la consulta y lo somete a la verificación correspondiente.
Antes que nada presentaremos los cálculos del proyecto encargado y del cual tiene las siguientes características:
- Edificio de 4 niveles de uso de oficina.
- Sobrecargas de acuerdo a la norma E-020
- Sistema aporticado
- Ubicado en Lima en suelo rigido.
- Distancia entre ejes de 6 m
- Vigas de 25×70, columnas 30×70 y losa aligerada de 20 cm.
MODELADO EN 3D EN PROGRAMA DE ANALISIS ESTRUCTURAL
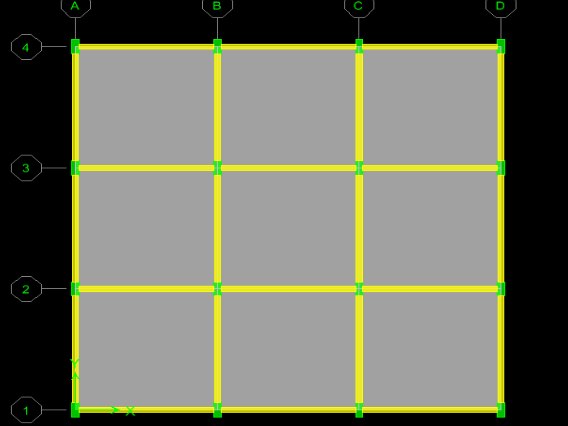
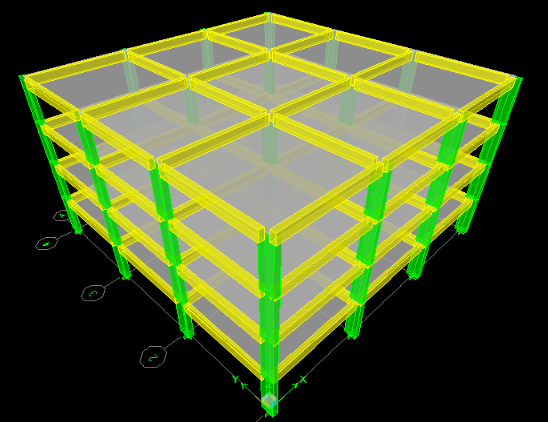
La zona afectada es la indicada a continuación:
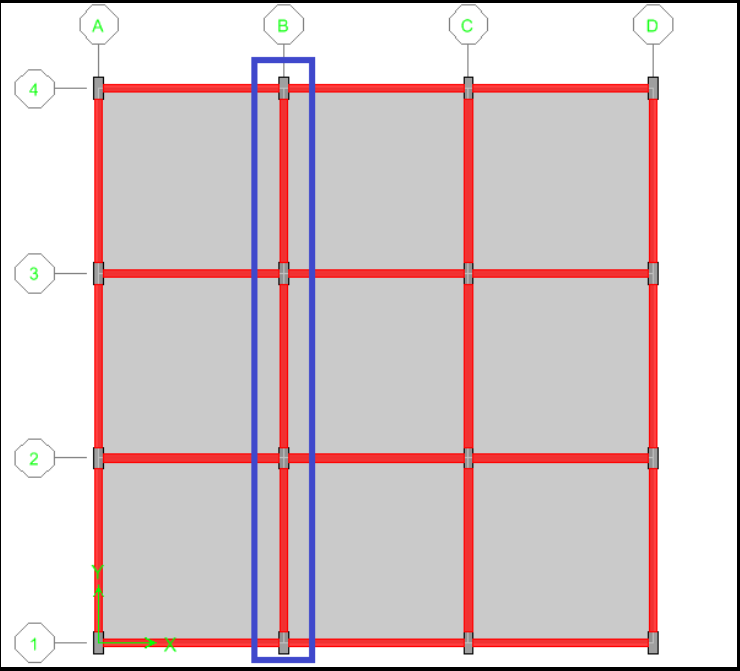
Antes de suscitarse el problema de obra el diseñador al tener ese eje, lo diseña teniendo en cuenta la siguiente envolvente de momentos:
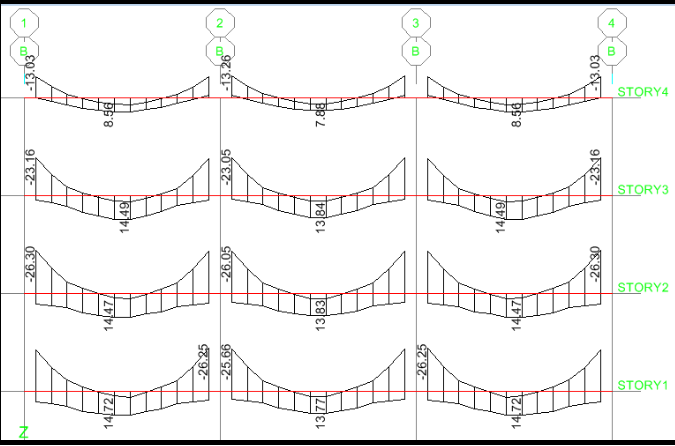


ACERO NEGATIVO MAS CRITICO: 16 cm2……… 8 φ 5/8”
ACERO POSITIVO MAS CRITICO: 7.7 cm2……… 4 φ 5/8”
ACEROCORRIDO SUPERIOR E INFERIOR: 2 φ 5/8”
Una vez concluido el diseño a flexión se continúa con el diseño a cortante.
Por fines de darle mayor ductilidad elegimos el siguiente
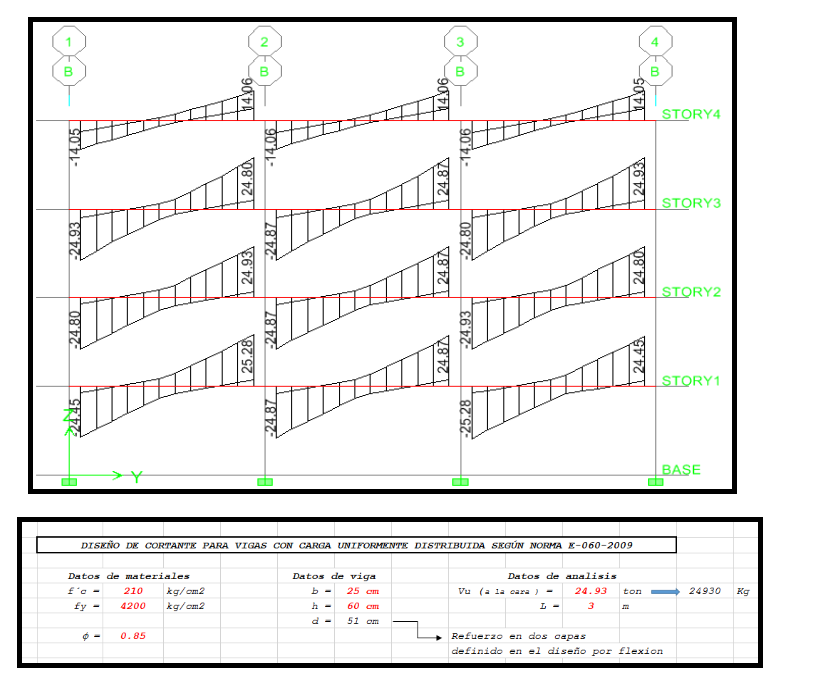
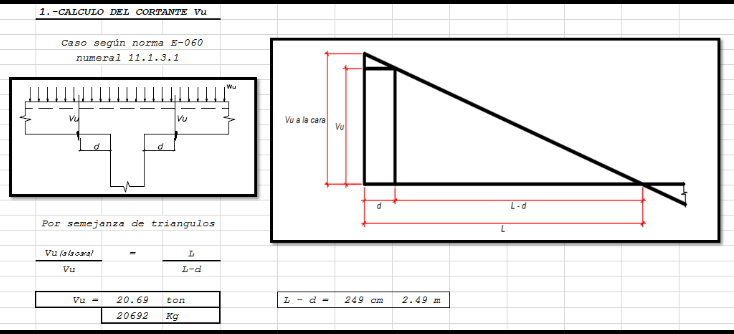
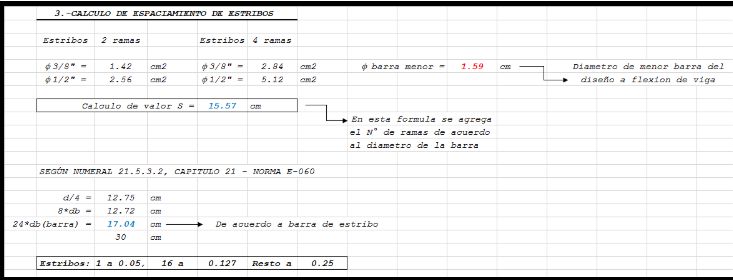
Estribaje: 1 a 0.05, 10 a .10, 8 a .12, resto a .25
Ahora enfocamos el problema con el contratista que llega con la noticia que las vigas del eje diseñado están con valores de resistencia del concreto en un promedio de f´c = 170 kg/cm2
Eso conlleva a que verifiquemos con obviamente una resistencia menor, pero también con un módulo de elasticidad reducido. Se muestra a continuación la reducción mencionada:
-Módulo de elasticidad de f´c = 210 kg/cm2
Ec = 15000*√210 = 217000 kg/cm
-Módulo de elasticidad de f´c = 170 kg/cm2
Ec = 15000*√170 = 195000 kg/cm
Para ello hacemos la entrada de las nuevas condiciones del material.
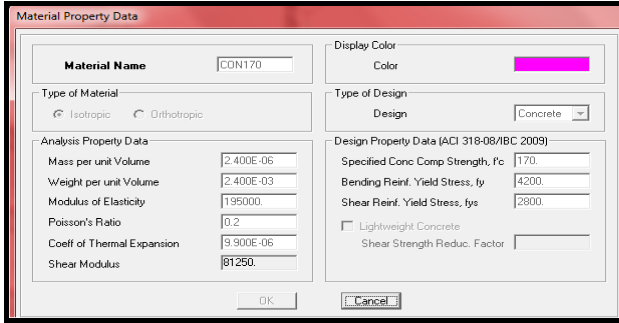
Del nuevo análisis estructural verificamos nuevamente los momentos flectores.
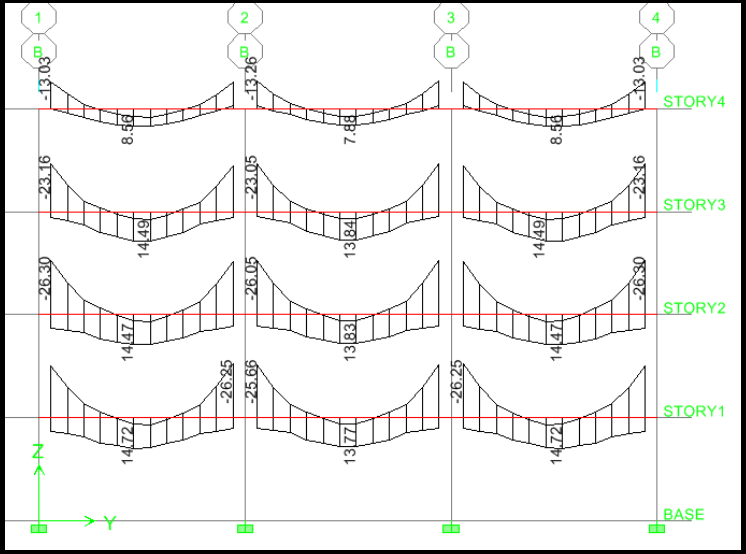
Se comprueba que los momentos flectores para la envolvente no han variado.
A continuación verificamos si por flexión aun el acero colocado cumple con los requisitos de diseño:
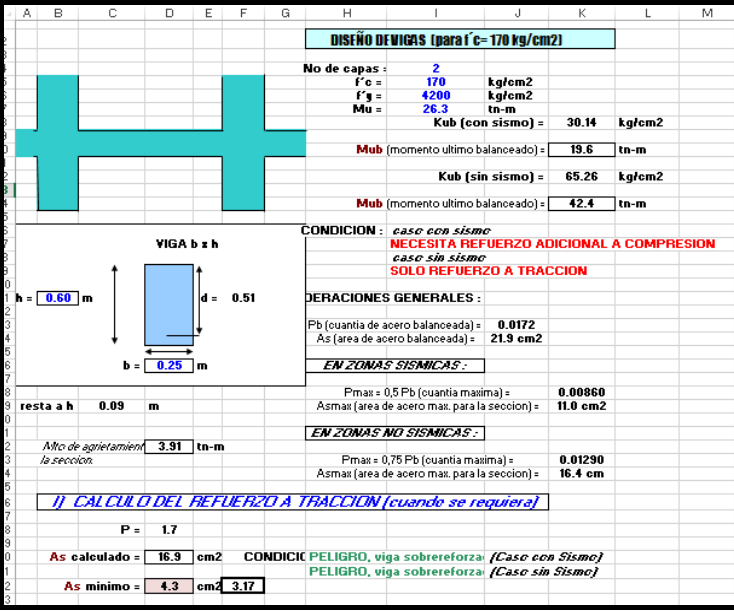
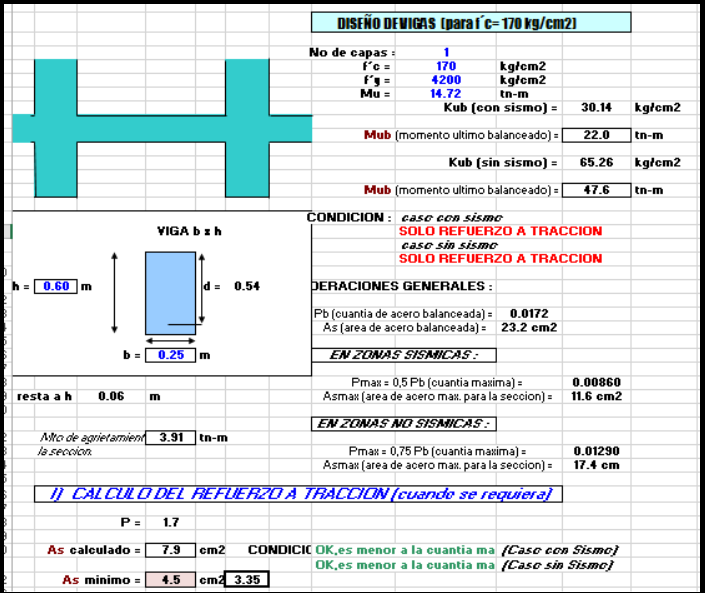
ACERO NEGATIVO MAS CRITICO: 16 cm2……… 8 φ 5/8” (Diseño original)
ACERO NEGATIVO MAS CRITICO: 16.9 cm2……… 8 φ 5/8” (Diseño verificado)
ACERO POSITIVO MAS CRITICO: 7.7 cm2……… 4 φ 5/8” (Diseño original)
ACERO POSITIVO MAS CRITICO: 7.9 cm2……… 4 φ 5/8” (Diseño verificado)
ACERO CORRIDO SUPERIOR E INFERIOR: 2 φ 5/8”
Una vez concluido la verificación se concluye que la resistencia a flexión no ha sido alterada por lo que los aceros aun cumplen con los requisitos de resistencia.
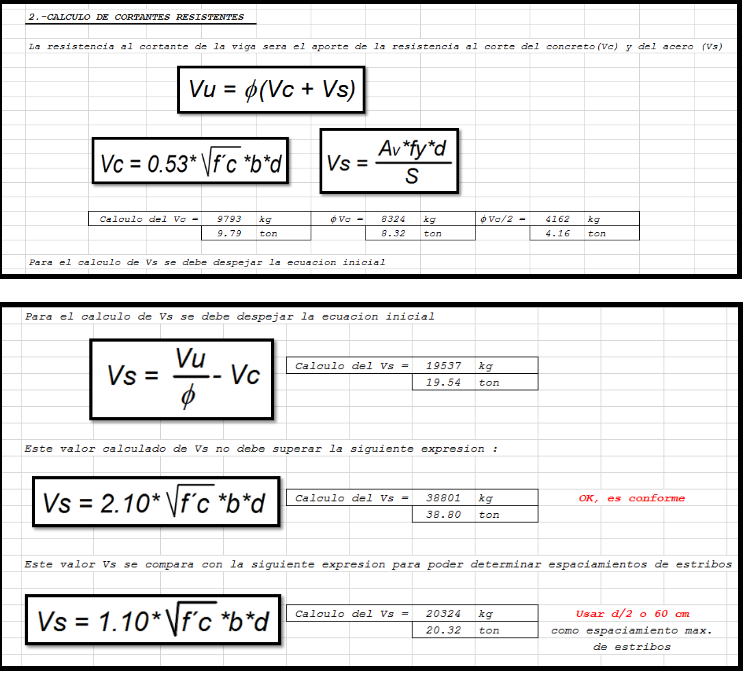
Procedamos a verificar la resistencia acortante.
Para este caso el valor φ = 1, pues al ya ser una estructura construida, la resistencia f´c, ya fue determinada. No sería ya factible aplicarle coeficientes de reducción.
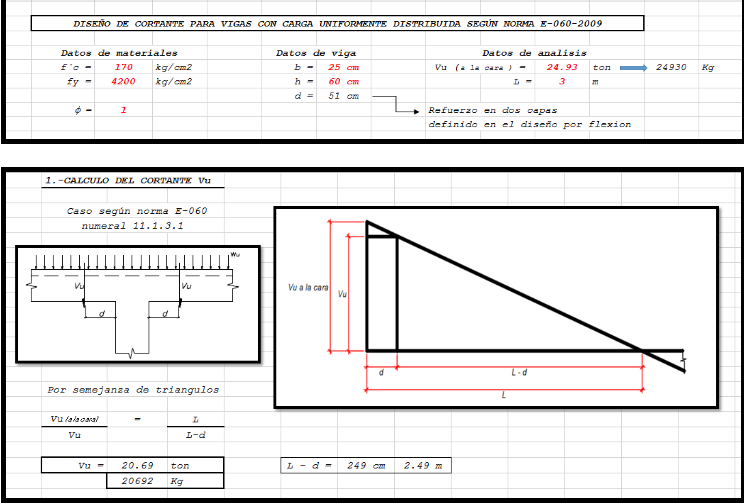
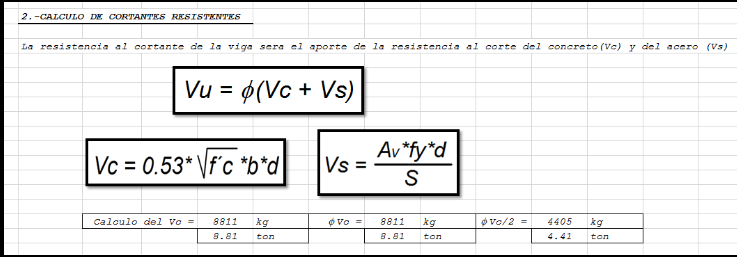
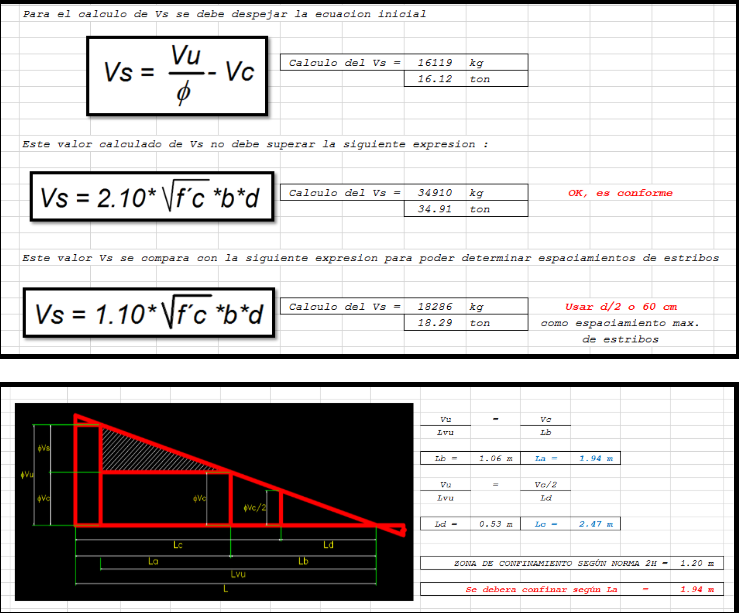
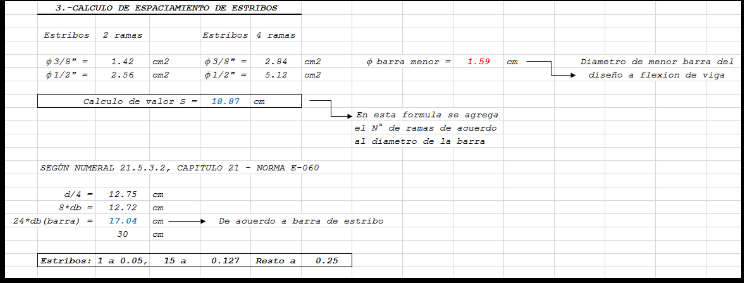
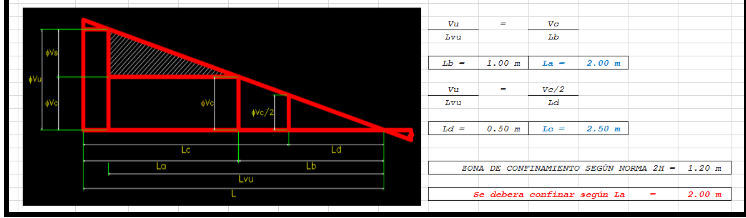
Se verifica que los estribos aún resisten el cortante.
Si bien el concreto ya no aporta mucho en valor. El acero y la distribución hecha por la norma en el capítulo 21 de diseño sismo-resistente, hace que se tenga una buena reserva de resistencia aportada por el acero, pese a la baja resistencia.
CONCLUSIONES
1.-En este artículo se ha demostrado que en un elemento sometido a flexión y corte como es el caso de una viga, el concreto tiene aporte no tan significativo y es el acero quien puede asumir mayores valores de carga.
2.-Se ha sacrificado un porcentaje del factor de seguridad al tener una resistencia de concreto menor al especificado en los planos.
3.-El valor bajo de resistencia del concreto no puede interpolarse a otros elementos como son las placas y columnas en las que las cargas axiales de compresión y tracción son más considerables. En este caso habrá que hacer las verificaciones correspondientes.
4.-En ninguna norma se especifica demoler las estructuras para el caso de bajas resistencias del concreto. Lo técnico es buscar las soluciones basadas en las normas de diseño. En caso de no cumplirse los requisitos de resistencia por las solicitaciones a la que está sometido el elemento existen los refuerzos estructurales como son las fibras de carbono, otras fibras, aditamentos metálicos, aumento de dimensiones, etc.
5.-Se puede pensar que en base al ejemplo mostrado se puede seguir cometiendo errores en el control de calidad del concreto, lo cual no es así. Mantener un adecuado control para poder tener una resistencia promedio al especificado en los planos, es menester para no seguir disminuyendo los factores de seguridad ante otras causas que puedan surgir en la vida útil de la estructura.
Bibliografía usada:
1.-Norma peruana de diseño de concreto armado E-060-2009
2.-Diseño de estructuras de concreto armado – Teodoro Harmsem – 5ta edición-Fondo editorial de Universidad Católica del Perú.
3.-Apuntes del curso de concreto armado – Gianfranco Otazzi – 2da edición-Fondo editorial de Universidad Católica del Perú.
4.-Diseño de estructuras de concreto armado – Antonio Blanco Blasco – 2da edición-Fondo editorial Colegio de Ingenieros del Perú.
5.-Serie de ensayos técnicos “Entendiendo el Concreto” – Ing. Enrique Pasquel Carbajal.
